Author: Haixiao Wang
As demonstrated in [1], expander graphs are a sparse graph that mimic the structure properties of complete graphs, quantified by vertex, edge or spectral expansion. At the same time, expander constructions have spawned research in pure and applied mathematics, with several applications to complexity theory, design of robust computer networks, and the theory of error-correcting codes.
This lecture is organized as follows. We introduce two different definitions of expanders in the first section, and then explore the relationship between them in second part.
17.1. Two Definitions
We start our discussion in expansion with two definitions of expansion: combinatorial and spectral. In the rest of this post, we consider an undirected graph  with
with 
, where self loops and multiple edges are allowed. Given two subsets 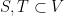 , the set of edges between
, the set of edges between  and
and  is denoted by
is denoted by 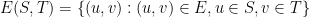 .
.
17.1.1. Combinatorial expansion
Intuitively, a graph 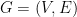 is an expander if subsets
is an expander if subsets 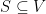 expand outwards into
expand outwards into  . In other words, all small subsets will have large boundary, respectively. Follow this intuition, we introduce the definition of boundary, based on edges and vertices respectively, to quantify the corresponding expansion.
. In other words, all small subsets will have large boundary, respectively. Follow this intuition, we introduce the definition of boundary, based on edges and vertices respectively, to quantify the corresponding expansion.
Definition 1(Boundary):
- The Edge Boundary of a set
 , denoted by
, denoted by  , is the set of edges
, is the set of edges  , which is the set of edges between disjoint set
, which is the set of edges between disjoint set  and
and  .
. - The Vertex Boundary of a set
 is a subset of vertices in
is a subset of vertices in  adjacent to vertices in
adjacent to vertices in  , denoted as
, denoted as 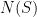 .
.
Obviously, vertex boundary  is the same as the number of neighboring vertices of vertex sets
is the same as the number of neighboring vertices of vertex sets  . With those notations, we then define the expansion over the entire graph
. With those notations, we then define the expansion over the entire graph 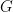 via maximizing over subsets
via maximizing over subsets  .
.
Definition 2(Expander): For some ![\varepsilon \in [0, 1]](https://s0.wp.com/latex.php?latex=%5Cvarepsilon+%5Cin+%5B0%2C+1%5D&bg=FFFFFF&fg=000&s=0&c=20201002) , a graph
, a graph  with
with  is an
is an
 -edge-expander if
-edge-expander if  .
. -vertex-expander if
-vertex-expander if 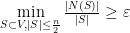 .
.
Remark 3: The reason for the restriction  is that we are examining the relative size of every cut in the graph, i.e., the number of edges crossing between
is that we are examining the relative size of every cut in the graph, i.e., the number of edges crossing between  and
and  , and we examine each case only once.
, and we examine each case only once.
Problem 1: Show that the complete graph  is
is
- at least a
 -edge-expander.
-edge-expander. - a
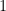 -vertex-expander. (We only consider
-vertex-expander. (We only consider ![\varepsilon \in [0, 1]](https://s0.wp.com/latex.php?latex=%5Cvarepsilon+%5Cin+%5B0%2C+1%5D&bg=FFFFFF&fg=000&s=0&c=20201002) here.)
here.)
From the definition above, the maximum  , which makes
, which makes  an
an  -edge-expander, is an important criteria, leading to the definition of Cheeger constant.
-edge-expander, is an important criteria, leading to the definition of Cheeger constant.
Definition 4(Cheeger Constant): The Edge Expansion Ratio, or Cheeger constant, of graph  with
with  , denoted by
, denoted by  , is defined as
, is defined as

Remark 5: Actually, Cheeger constant can be defined alternatively as 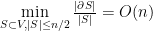 . We didn’t follow this definition since we want to keep
. We didn’t follow this definition since we want to keep ![\varepsilon\in [0, 1]](https://s0.wp.com/latex.php?latex=%5Cvarepsilon%5Cin+%5B0%2C+1%5D&bg=FFFFFF&fg=000&s=0&c=20201002) .
.
17.1.2. Spectral Expansion
To simplify our discussion, we focus on regular graphs in the rest of this lecture. Let  denote the adjacency Matrix of a
denote the adjacency Matrix of a 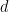 -regular graph
-regular graph  with
with  and
and 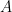 being real symmetric, then
being real symmetric, then 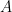 has
has 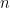 real eigenvalues, denoted by
real eigenvalues, denoted by  , and corresponding orthonormal eigenvectors
, and corresponding orthonormal eigenvectors 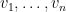 with
with  . The spectrum of
. The spectrum of 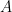 encodes a lot of information about the graph structure. Recall the following properties, which we have seen in previous lectures.
encodes a lot of information about the graph structure. Recall the following properties, which we have seen in previous lectures.
- The largest eigenvalue is
 and the corresponding eigenvector is
and the corresponding eigenvector is 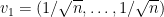 .
. - The graph
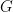 is connected if and only if
is connected if and only if 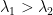 .
. - The graph is bipartite if and only if
 .
.
The definition of spectral expansion and spectral gap then follows.
Definition 6(Spectral Expansion): A graph  with
with  is a
is a 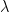 -spectral-expander if
-spectral-expander if  .
.
In other words, the second largest eigenvalue of  , in absolute value, is at most
, in absolute value, is at most 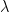 . This also gives rise to the definition of Ramanujan graph.
. This also gives rise to the definition of Ramanujan graph.
Definition 7(Ramanujan graph): A connected 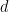 -regular graph
-regular graph 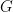 is a Ramanujan graph if
is a Ramanujan graph if 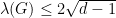 .
.
We now refer to the spectral gap.
Definition 8(Spectral Gap): The spectral gap of 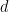 -regular graph
-regular graph 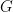 is
is  .
.
Remark 9: Sometimes the spectral gap is defined as 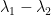 , which is often referred as one-sided.
, which is often referred as one-sided.
Problem 2:
- Show that the complete graph
 has spectral gap
has spectral gap 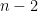 . Actually, we can also show that the one-sided spectral gap is
. Actually, we can also show that the one-sided spectral gap is 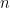 .
. - Show that the complete bipartite graph
 has spectral gap
has spectral gap  . (Hint: use the spectral property above.)
. (Hint: use the spectral property above.)
17.2. Relating Two Definitions
It is not so obvious that the combinatorial and spectral versions of expansion are related. In this section, we will introduce two relations between edge and spectral expansion: the Expander-Mixing Lemma and Cheeger’s inequality.
17.2.1. The Expander-Mixing Lemma
Lemma 10(Expander-Mixing Lemma[2]): Let  be a
be a 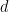 -regular graph with
-regular graph with 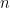 vertices and eigenvalues
vertices and eigenvalues  . Then for all
. Then for all 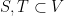 :
:
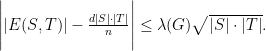
As we can see, the left-hand side measures the deviation between two quantities:
 : the number of edges between the two subsets
: the number of edges between the two subsets  and
and  .
. : the expected number of edges between two subsets
: the expected number of edges between two subsets  and
and  , drawn from an Erdos–Renyi random graph
, drawn from an Erdos–Renyi random graph 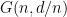 .
.
The Expander-Mixing lemma tell us a small  (a.k.a. large spectral gap) implies that this discrepancy is small, leading to the fact that the graph is nearly random in this sense, as discussed in [1]. We should mention that the converse of expander-mixing is true as well, stated as follows.
(a.k.a. large spectral gap) implies that this discrepancy is small, leading to the fact that the graph is nearly random in this sense, as discussed in [1]. We should mention that the converse of expander-mixing is true as well, stated as follows.
Lemma 11(Expander-Mixing Lemma Converse [4]): Let  be a
be a 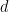 -regular graph with
-regular graph with 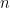 vertices and eigenvalues
vertices and eigenvalues  satisfying:
satisfying:

for any two disjoint subsets 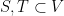 and some positive
and some positive  . Then
. Then  .
.
Proof of Expander-Mixing Lemma: Recall that the adjacency matrix 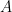 has eigenvalues
has eigenvalues  with corresponding orthonormal eigenvectors
with corresponding orthonormal eigenvectors 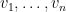 . Let
. Let 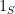 and
and  be the characteristic vectors of subsets
be the characteristic vectors of subsets  and
and  (a.k.a., the
(a.k.a., the  -th coordinate of
-th coordinate of 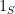 is
is 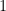 if
if  and
and  otherwise). We then decompose
otherwise). We then decompose 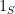 and
and  in the orthonormal basis of eigenvectors
in the orthonormal basis of eigenvectors 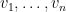 as
as
 .
.
Observing that  , we expand out the right hand side and apply orthogonality, which yields
, we expand out the right hand side and apply orthogonality, which yields
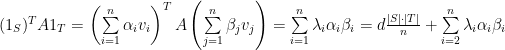 .
.
where the last step follows from the facts  with corresponding
with corresponding 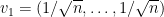 ,
,  and
and 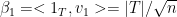 . Shifting the first term on right hand side to the left, the desired result follows from Cauchy-Schwarz inequality:
. Shifting the first term on right hand side to the left, the desired result follows from Cauchy-Schwarz inequality:

Remark 12: If we normalize the adjacency matrix  and obtain
and obtain  , where each entry of
, where each entry of 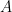 is divided by
is divided by 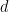 , then the corresponding eigenvalues of
, then the corresponding eigenvalues of  , namely
, namely  , lie in the interval
, lie in the interval ![[-1, 1]](https://s0.wp.com/latex.php?latex=%5B-1%2C+1%5D&bg=FFFFFF&fg=000&s=0&c=20201002) . The Expander-Mixing Lemma is in the form of
. The Expander-Mixing Lemma is in the form of

It is sometimes convenient to consider the normalized spectrum. For example in random graph theory, it would be convenient to look at the normalized spectrum when the expected degree  . However, we can focus on the spectrum of $\latex A = A(G)$ without normalization when the expected degree $\latex d = O(1)$.
. However, we can focus on the spectrum of $\latex A = A(G)$ without normalization when the expected degree $\latex d = O(1)$.
Regular 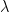 -spectral expanders with small
-spectral expanders with small  (a.k.a. large spectral gap) have some of significant properties, listed as follows.
(a.k.a. large spectral gap) have some of significant properties, listed as follows.
Corollary 13: An independent set , in a graph  with
with  , is a set of vertices
, is a set of vertices  , where no two vertices in
, where no two vertices in  are adjacent, i.e. with
are adjacent, i.e. with 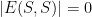 . An independent set
. An independent set  , in a
, in a 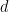 -regular
-regular 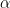 -spectral expander
-spectral expander 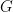 , has cardinality at most
, has cardinality at most 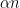 , i.e.,
, i.e., 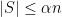 , which follows immediately from Lemma 10(Expander-Mixing Lemma[2]).
, which follows immediately from Lemma 10(Expander-Mixing Lemma[2]).
Corollary 14: Given a graph  with
with  , the diameter of
, the diameter of 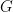 is defined as
is defined as  , where
, where  is the length of shortest path between
is the length of shortest path between  and
and  . If
. If 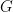 is a
is a 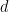 -regular
-regular 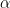 -spectral expander
-spectral expander 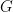 with
with  , then we have
, then we have

17.2.2. Cheeger’s Inequality
As we have seen from previous discussion, spectral expansion implies strong structural properties on the edge-structure of graphs. In this section, we introduce another famous result, Cheeger’s inequality, indicating that the Cheeger constant(Edge Expansion Ratio) of a graph 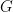 can be approximated by the its spectral gap
can be approximated by the its spectral gap  .[6]
.[6]
Theorem 15(Cheeger’s inequality, [3]): Let  be a
be a 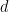 -regular graph with eigenvalues
-regular graph with eigenvalues  , then
, then
 .
.
In the normalized scenario  with eigenvalues
with eigenvalues ![\bar{\lambda}_{1}, \cdots, \bar{\lambda}_n \in [-1, 1]](https://s0.wp.com/latex.php?latex=%5Cbar%7B%5Clambda%7D_%7B1%7D%2C+%5Ccdots%2C+%5Cbar%7B%5Clambda%7D_n+%5Cin+%5B-1%2C+1%5D&bg=FFFFFF&fg=000&s=0&c=20201002) , we have
, we have
 .
.
Remark 16: The proof for the normalized scenario is different from the regular scenario. We should start from the desired quantity and finish the calculation step by step. However, the strategy are the same. We use the Rayleigh Quotient to obtain upper bound and lower bound.
In the context of  , the estimate of spectral gap was given by Nilli Alon.
, the estimate of spectral gap was given by Nilli Alon.
Theorem 17([5]): For every 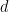 -regular graph
-regular graph 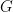 , we have
, we have

The 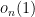 term is a quantity that tends to zero for every fixed
term is a quantity that tends to zero for every fixed 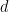 as
as 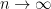 .
.
[1]. Shlomo Horry, N. L. and Wigderson, A. (2006). Expander graphs andtheir applications.BULLETIN (New Series) OF THE AMERICAN MATHEMATICAL SOCIETY, 43(4).[2]. Alon, N. and Chung, F. R. K. (1988). Explicit construction of linear sized tolerantnetworks.Discrete Mathematics, 42 [3]. Cheeger, J. (1970). A lower bound for the smallest eigenvalue of the laplacian.Problems inanalysis, 26.[Nilli, 1991] Nilli, A. (1991). On the secon[4]. Yonatan Bilu, N. L. (2006). Lifts, discrepancy and nearly optimal spectral gap.Com-binatorica, 26[5]. Nilli, A. (1991). On the second eigenvalue of a graph.Discrete Mathematics, 91(2):207–210.[6]. Lovett, S. (2021). Lecture notes for expander graphs and high-dimensional expanders.
. Annals of Mathematics 18 (1916), p. 70-73.